نبوغ بولتزمن در ترمودینامیک
نبوغ بولتزمن در ترمودینامیک
ترجمه : حمیدرضا صفری
فیزیک جدید! لودویگ بولتزمن، نه تنها پدر فیزیک آماری، بلکه متخصص ترمودینامیک نیز بود. این داستان درباره این است که چگونه نام او در قانون استفان-بولتزمن ظاهر شد. بیایید با خود قانون شروع کنیم که در مورد نور ساطع شده از اجسام داغ؛ مانند میلههای گداخته یا خورشید صحبت می کند. به ویژه، توان تابشی (انرژی بر واحد زمان) را در نظر بگیریم که یک جسم بر واحد سطحش گسیل میکند. این کمیت گسیل تابشی نامیده میشود.

در سال ۱۸۷۹ میلادی، جوزف استفان به طور تجربی نشان داد که گسیل تابشی متناسب با توان چهارم دما[یِ جسم] است: j= σT⁴ . هر چقدر جسمی داغتر باشد،انرژی بسیار بیشتری گسیل میکند.

دانشجویان فیزیک جدید یاد میگیرند که این قانون به عنوان نتیجه سادهای از قانون طیف جسم سیاه پلانک بهدست میآید؛ قانون طیف جسم سیاه میگوید چقدر توان بر واحد سطح و در هر طول موج گسیل میشود. به این معنا که برای رنگهای مختلف چقدر نور دریافت میکنیم.
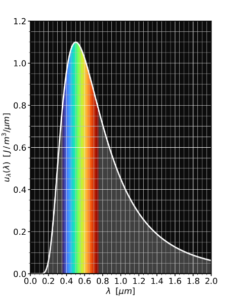
همه چیزی که نیاز دارید این است که روی فرمول پلانک برای همه طول موجها انتگرال بگیریم و درنهایت فرمول استفان-بولتزمن را بهدست آوریم j = σT⁴.
چیزی که موضوع را جذاب میکند این است که پلانک این طیف جسم سیاه را در سال ۱۹۰۰ میلادی بهدست آورد و برای این کار نیاز به ابداع ایدهای کلیدی از مکانیک کوانتومی داشت: فوتونها. اما بولتزمن تفسیرش از موضوع را ۱۶ سال زودتر و در سال ۱۸۸۴ میلادی منتشر کرد! او چطور قادربود این کار را انجام دهد؟
بولتزمن از یک استدلال زیبای ترمودینامیکی استفاده کرد که برای آن نیازی به دانستن مکانیک کوانتومی نداشت. در ادامه مطالبی در مورد ریاضیات و ترمودینامیک خواهد آمد ولی سعی شده که آنها دلپذیرتر شوند!!!
بولتزمن بحث خود را با سه ایده شروع کرد:
(۱) تابش گرمایی به عنوان یک سیستم ترمودینامیکی، « فزونبر» است
(۲) فشار برابر با ۱/۳ چگالی انرژی تابشی است
(۳) پتانسیل شیمیایی برابر صفر است.
اوه اوه. ولی اینها چه معنایی میدهند؟
به زبان ساده ایده اول میگوید که محتوای انرژی تابشی با اندازه جسم چند برابر میشود. اگر دو اجاق داغ با دمای یکسان داشته باشید، که با تابش گرمایی اشباع شده باشند و حجم دومی دو برابر اولی باشد، در نتیجه تابش دومی حاوی دو برابر انرژی اولی است. ایده دوم مفهوم «فشار تابشی» را کمّی میکند: نور میتواند شما را هل دهد! ماکسول در سال ۱۸۷۴ میلادی متوجه شد که این نتیجهای از معادلاتش است و دو سال بعد آدولفو بارتولی استدلال ترمودینامیکی برای آن ارائه داد که بولتزمن آن را شنیده بود. ایده سوم زیرکانهترین آنها است: پتانسیل شیمیایی μ اساسا هزینه ترمودینامیکی اضافه کردن یک ذره به سیستم را توصیف میکند. اما سر و کله ذرات در تابش چگونه پیدا میشود؟ بولتزمن چیزی در مورد فوتونها نمیدانست!
من هرگز متوجه نشدم که استدلال بولتزمن دقیقا به چه صورت بوده است، اما او باید شهوداً ذره نبودن نور را به معنی صفر شدن پتانسیل شیمیایی μ در نظر گرفته باشد. در اصطلاح مدرن میگوییم «تعداد فوتون ها پایسته نیست». ممکن است این فقط یک حدس خوششانس بوده باشد؟
در هر صورت، با در نظرداشتن این سه ایده ما آماده حرکت هستیم! بولتزمن بررسی خود را با در نظر گرفتن انرژی داخلی به عنوان تابعی از متغیرهای ترمودینامیکی مجاز: دما T، حجم V، و پتانسیل شیمیایی μ شروع میکند. این را میتوان به این صورت نوشت (U(T, V, μ.
اگر طبق ایده ۳ بپذیریم که پتانسیل شیمیایی صفر میشود، میتوان از μ صرف نظر کرد و فقط نوشت (U(T,V. و همچنین اگر فرض کنیم که سیستم فزونبر است، طبق ایده ۱، انرژی داخلی باید متناسب با حجم باشد: (U(T,V) = V u(T که فقط به تابع نامعلومی از دما وابسته است.
همچنین فزونبری سیستم ترمودینامیکی ایجاب میکند که معادلات اویلر برقرار باشند: U = TS – PV + μN. این نتیجهای از ویژگی توابع همگن است («همگن» بودن نتیجهای از «فزونبر» بودن است). در این رابطه S آنتروپی است که نقش برجسته آن به زودی روشن میشود.
تنها یک ایده دیگر باقی میماند، [ایده] شماره ۲، که میگوید فشار برابر با ۱/۳ چگالی انرژی است. این منجر میشود به اینکه به دست آوریم:
P = (⅓)U/V = (⅓)u(V/V) = ⅓u
حالا بیایید همه اینها را با هم در نظر بگیریم! وقتی μ = 0 میتوانیم در معادله اویلر از جمله μN صرفنظر کنیم و عبارت دوم در آن را با استفاده از PV = U/3 جایگزین کنیم تا عبارت جدید U = TS – U/3 را بهدست آوریم. سپس میتوانیم این عبارت را بر حسب انتروپی حل کنیم: S = 4U / 3T = (4V/3) u(T)/T .
آخرین نبوغی که بولتزمن به کار برد، استفاده از یک «رابطه ماکسول» بود، یکی از این شروط انتگرالپذیری که همواره تنفربرانگیز ولی کاملا بدیهی هستند و بدون هزینهای برای هر پتانسیل ترمودینامیکی اضافه میشود.
با صرف نظر کردن از تعداد ذره و پتانسیل شیمیایی ( μ = 0 )، انرژی آزاد یک سیستم تابعی از دما و حجم سیستم است: (F(T,V. این یک پتانسیل ترمودینامیکی است چون میتوانیم انتروپی و فشار را با مشتق گیری از آن به دست آوریم:
S = –dF/dT و P = –dF/dV. این روابط اصلی در ترمودینامیک هستند. ترفند این است که دوباره از انتروپی S نسبت به حجم V و از فشار P نسبت به دما T مشتق بگیریم. هر دوی اینها مشتق مرتبه دوم پتانسیل ترمودینامیکی F بوده که با هم جابجا میشوند! و بنابراین جوابها باید مانند هم باشند!
به عبارت دیگر، تساوی dS/dV)_T = (dP/dT)_V) را به دست میآوریم که اندیسهای “_T” و “_V” یادآور متغیرهای دیگری هستند که ما نسبت به آنان مشتق نگرفتیم. حالا فقط باید عبارتی که قبلا برای تابش گرمایی به دست آوردیم را در این تساوی وارد کنیم.
اول از همه اگر P = u(T)/3 سپس داریم (dP/dT)_V = u’(T)/3 که «’» نشان دهنده مشتق نسبت به دما است. و اگر S = (4V/3) u(T)/T سپس به دست میآوریم (dS/dV)_T = (4/3) u(T)/T . ولی این دو عبارت با هم مساوی هستند! با حذف ۱/۳ ما به عبارت u’(T) = 4 u(T)/T میرسیم.
توجه کنید که چه کاری انجام دادیم! ما معادله دیفرانسیلی برای (u(T به دست آوردیم! در واقع، یک معادله ساده که یک حل توانی دارد و بلافاصله جوابی به صورت u(T) = a T⁴ به دست میآید که در آن «a» ثابت دلخواه انتگرالگیری است.
اساسا این جواب ما است! برای به دست آوردن نتیجه نهایی، از این استفاده میکنیم که گسیل تابشی برابر (j(T) = ¼cu(T است، که در آن c سرعت نور است. چرا اینطور است؟ چون که همیشه شار با چگالی چیزی که شارش می شود ضربدر سرعت شارش آن، برابر است که در اینجا سرعت شارش، سرعت نور است!
و ضریب ۱/۴ از کجا می آید؟ خب، این ضریب اولا به این علت ظاهر میشود که ما به شاری علاقهمندیم که به طرف ما می آید نه به شاری که در جهت خلاف حرکت می کند(یک ضریب ۱/۲). همچنین لازم است که همه زوایا در جهت عمود بر سطح تصویر شوند (ضریب ۱/۲ دوم).
نکته اساسی این است که ما وابستگی به T⁴ را، تنها از ملاحظات ترمودینامیک به دست آوردیم! چطور توانستیم این نتیجه را بدون مفاهیم «مکانیک کوانتومی» بهدست آوریم؟
دو پاسخ برای آن وجود دارد. اول اینکه این مفاهیم در پس ایدههایی که بولتزمن بر آنها تکیه کرد (معادلات حالت) پنهان شدهاند. شاید مهمترین آنها μ = 0 باشد. و دوم در ثابت نامعلوم انتگرالگیری a مخفی شده است.
یکی از نتایج جذاب قانون پلانک، پیشبینی ضریب قانون استفان-بولتزمن است. و البته این ضریب شامل ثابت پلانک هم میشود! هیچ راهی وجود ندارد که بولتزمن بتواند آن را وارد کند که البته نیازی به این کار نداشت!
به سختی میتوان زیبایی این استنتاج را شرح داد. هندریک آ. لورنتز این استنتاج را «مروارید واقعی فیزیک» نامید. در حقیقت، لورنتز اولین کسی بود که نام بولتزمن را به قانون استفان-بولتزمن اضافه کرد. اجازه دهید که با یک دیدگاه «فلسفی» تر نتیجه گیری کنم (دیدگاهی که برای من بسیار عزیز است). این حقیقت که بولتزمن توانست این قانون را بهدست آورد (که ریشه های مکانیک کوانتومی عمیقی دارد)، بدون دانستن چیزی در مورد مکانیک کوانتومی، موضوعی بسیار عمیق و ژرف است. این قانون از قدرت واقعی ترمودینامیک صحبت میکند که به ما اجازه میدهد قوانین طبیعت را تبیین و کشف کنیم البته بدون دانستن جزییات «جهان میکروسکوپی» که از آن ساخته شدهاند. ما همیشه نیاز نداریم تا بدانیم چه اتفاقی در «اعماق زیرین» در حال رخ دادن است! به همین دلیل است که بازده کارنوی ماشین گرمایی یک حد جهانی است و ما را ملزم نمیکند که به جزئیات موتور فکر کنیم. به همین علت است که «ترمودینامیک سیاهچاله» به ما اجازه میدهد تا درباره مفاهیمی مثل آنتروپی، سطح و تابش سیاهچاله، بدون اینکه نظریه گرانش کوانتومی کاملا ساختار یافته را در اختیار داشته باشیم، استدلال کنیم، و به این دلیل است که در مورد قانون استفان-بولتزمن میتوانیم ویژگیهای مهم تابش گرمایی را درک کنیم، بدون آنکه طبیعت کوانتومی نور را کاملا فهمیده باشیم.
معتقدم که باید بپذیریم که این امر در فیزیک، طبیعی است. به خصوص اگر روی «مرز میکروسکوپی»، به دنبال قوانین اساسی جدید (ریسمانها، ابرتقارن، هولوگرافی و …)، باشید.
داشتن مفاهیمی مثل ترمودینامیک که در غیاب درک میکروسکوپی مانند فانوس روشن عمل میکند، فوقالعاده ارزشمند است. به همین دلیل است که ترمودینامیک تنها سرگرمی عجیب فیزیکدانان باستانی، که در مورد موتورهای حرارتی فکر میکردند، نیست.
اگر روی مرز و لبه دانش کار میکنید، دانستن آن برای شما ممکن است سودمند باشد! و به همین دلیل است که ما باید به آموزش آن، نه فقط به عنوان موضوعی در دنباله فیزیک آماری، بلکه به عنوان مجموعه ای ارزشمند از ایدهها و نیز به خاطر ارزش خودشان ادامه دهیم.
منبع:
https://twitter.com/MarkusDeserno/status/1512822212646125569

